
The Ultimate Guide
Score a perfect 170 in GRE Math
A perfect 170 score on the GRE Math section guarantees that you’ll stand out. But even the best, the brightest of us wonders if a perfect 170 is possible. What GRE math prep techniques can you employ to ensure you save time? What common pitfalls should you be wary of?
This and more is what we’re going to discuss today.
Table of Contents
Chapter 1
GRE Math Syllabus
Which of us here does NOT want a centum? A perfect score on the GRE Math section, especially considering most of you are looking at applying to top universities. But there’s always the fear that this just isn’t possible. Even the best, the brightest of us wonders if a perfect 170 on the GRE Mathematics is possible. We’re here to break this fear, to tell you it IS possible.
This fear would appear justified. It’s very easy and quite common to make silly mistakes on an exam like the GRE. Somehow we’ve internalized that a perfect score is just not possible. Let’s change that.
GRE Math Syllabus:
Most of you are familiar with the pattern of the GRE. The GRE Math syllabus includes topics such as arithmetic, algebra, geometry and data analysis.
Now, these are all very, very general topics. Arithmetic means number systems, properties of integers, you have ratios & proportions. You have absolute values.
With respect to algebra – you have linear equations, linear inequalities, algebraic expressions absolute values yet again, inequalities and everything.
Geometry -you have everything right from lines and angles, circles, two-dimensional figures to three-dimensional geometry.
Data analysis – the stuff that you have learned in school is all that’s covered. No higher level of mathematics is tested on the GRE. So it’s going to be easier for you if you recap the concepts you first learned in school.
These concepts and enough practice are all that’s required to get that 170 GRE Math score.
The ETS tends to lay more weightage on arithmetic and data analysis. By this we mean, suppose you have 20 questions in each section, you might have close to ten or fourteen questions only on arithmetic and data analysis.

The remaining questions will be divided between algebra and geometry, so prepare well, focus more on these two topics.
[bctt tweet=”GRE Math Trip : Arithmetic and data analysis have a lot more weightage in GRE Math. So attend these Qs first followed by the rest : Geometry and Algebra ” username=”galvanizeprep”]
That doesn’t mean that you just have to ignore algebra and geometry. You have to go through this because we’re looking at nothing less than 170. This is for people who don’t have time. Go for arithmetic and data analysis first and then just go through algebra and geometry. Why? All of the tough or difficult questions on the GRE are taken from these two topics.
Also, focusing on arithmetic will make learning algebra easier by because algebra is nothing but arithmetic with variables.
For Geometry, you have to play around with figures, visual interpretation. Look at the figure, read the question and try to interpret it.
The GRE is a skill-based exam, it doesn’t test solely your knowledge. A large part of how well you perform on the GRE will have to do with your understanding of the underlying concepts being tested.
If your grasp of the concepts is strong, you’re guaranteed a high score of 165+. Knowledge of the GRE math formulas accounts accounts for maybe the remaining 5 points alone. This, just to emphasize that simply knowing the formulae is not enough for a perfect 170.
Chapter 2
Mistakes you need to Avoided to Score 170 in GRE Math
To get to a perfect 170, you need to avoid making any errors. Typically, test-takers are prone to making two types of mistakes – calculation errors and conceptual errors.
1. Calculation Based Mistakes:
So what are these calculation-based mistakes? These include not reading the question correctly, misinterpreting what is asked in the question because you did not read it properly. Calculating what has not been asked for thus wasting time. This is a very common pitfall test-takers fall into. Not using the right GRE math formula.

This, accounts for a meager 2% of errors, however. As we’ve said, the GRE does not test your knowledge of formulae. Most questions require you to apply the concepts you’re supposed to have learned and got to the answer. Not rounding off correctly.
Again, this might be because you didn’t read the question correctly. Sometimes they mention in the question to what degree you’re required to round off the answer to. Let’s take a look at an example of a GRE math problem now.
“How many solutions will the equation ‘x^2 – 2x + 1 = 0 have’?”
Now a lot of test-takers look at the question and jump to the conclusion that the answer is B.(2) Since you’re only reading this, you’re probably not too panicked right now. You probably know that because this is a quadratic equation, the answer is A (2).
They’re not asking how many distinct solutions or how many equal solutions there are. Since its a quadratic equation, the answer will always be 2.
If you’re not focused on the day of the GRE, you might make the mistake mentioned above and think that the GRE is such a complicated exam.
That they would not possibly ask such simple questions like this, so they’ll start doing some factorization immediately.
Not even the straightforward kind – but a^2 + b^2 – 4ac. All this because they didn’t read the question properly. To quote Albert Einstein – “If I had 60 minutes to solve a problem, I’d spend 55 minutes defining it and 5 solving it.”
Just to recap, the correct answer to that question is 2. A quadratic equation always has two solutions. Nowhere did they ask for identical or distinct questions. Reading the question correctly would’ve saved you from calculating for the answer.
The next one is rounding off errors. Another very common type. Let’s look at yet another example. Suppose the question says ‘round it off to two decimal places.’ The answer that needs rounding off is 12.346.
Rounding off doesn’t mean trimming the answer. Normally, these types of questions tend to be of the Numeric Entry type. As you know, there are four types of question on the GRE Math section: Numeric Entry, MCQs, MAQs, and Quantitative Comparison questions.
Coming back to the example, your answer should be 12.35. If your answer is 12.34, you’re wrong. When rounding off, you look at the number to the right.
If this value is equal to or greater than 5, you will round off the figure in question up to the hundredth digit. That is the meaning of rounding off.
Most of you might think this is quite obvious but during the exam, if you start to panic or worry, you might end up truncating or trimming the answer which is wrong.
Keep that in mind. We’ve covered calculation mistakes. These stem largely from not reading the question correctly and rounding off incorrectly.
2. Conceptual Mistakes:
Conceptual mistakes in GRE math are very common in geometry and data analysis. Let’s look at an example (in the video above). There are two triangles drawn, both crudely, as you can see.
For the geometry, there is one very important rule you need to keep in mind – Do not base any assumptions off of just a visual representation. If you look at the triangle in the image, it looks as though AB is perpendicular to BC. Never ever jump to that conclusion.
Unless there’s a question statement that says ‘angle b is equal to ninety.’ or the figure itself contains the perpendicular symbol, do not assume this.
It might look like AB is perpendicular to BC but there’s no way you can know this for sure unless it’s been specified. This is a very common error made in geometry.
Figures are not always drawn to scale.If they are, it will be specified, but most of the figures are not not drawn to scale.
The other thing you should focus on is the information given above or below the figure. For example, suppose you have a right angle triangle that’s given to you.
Sometimes one of the angles, angle c might be equal to sixty degrees.
This might not be mentioned in the question but it could be specified around the image so please scrutinize the figure properly so that it’s easier for you to answer this.
This again boils down to not reading the question correctly.
Let’s look at data analysis now. What kind of conceptual errors are usually made with reference to data analysis type questions? Most questions involve data interpretation and permutations & combinations.
The most common mistake made here is the inability to differentiate between permutations & combinations.
What to use when. So if you do not know this, you’re probably going to make mistakes in probability as well.
So these mistakes occur because you’re not totally comfortable with the concepts of permutation, combination & probability. How do you understand a concept thoroughly though?
One way to do this is to take as many GRE math practice problems as possible and then review your mistakes.
By doing this, you’ve learned firsthand what NOT to do the next time you’re faced with such a question. The other way to do this is to go over the concept repeatedly until you’ve familiarized yourself to a great deal. We do not recommend the latter.
Take as many GRE Math practice tests as possible and when you find yourself held up, return to review the concept.
Look at the concept, come back and look at the GRE Math problem again. Review. For every test you take, it is very important to review your math performance. It is not enough to attempt several hundred questions without reviewing them.
Let’s look at data analysis now. What kind of conceptual errors are usually made with reference to data analysis type questions? Most questions involve data interpretation and permutations & combinations. The most common mistake made here is the inability to differentiate between permutations & combinations.
What to use when. So if you do not know this, you’re probably going to make mistakes in probability as well. So these mistakes occur because you’re not totally comfortable with the concepts of permutation, combination & probability. How do you understand a concept thoroughly though? One way to do this is to take as many practice tests as possible and then review your mistakes.
By doing this, you’ve learned firsthand what NOT to do the next time you’re faced with such a question. The other way to do this is to go over the concept repeatedly until you’ve familiarized yourself to a great deal. We do not recommend the latter. Take as many practice tests as possible and when you find yourself held up, return to review the concept.
Look at the concept, come back and look at the problem again. Review. For every test you take, it is very important to review your performance. It is not enough to attempt several hundred questions without reviewing them.
[bctt tweet=”Mistakes in GRE Math : Calculation Error and Conceptual Errors. Also make sure to read the questions very carefully and be careful while rounding off answers” username=”galvanizeprep”]
Chapter 4
Important Techniques
GRE Math Practice:
Let’s look at some important techniques that you need to follow to get this perfect 170. A GRE Math cheat sheet. Time management. Reading the question properly. Implement ZONEF, PIES. Apply shortcuts, go for approximations. Back-substitute in MCQ & MAQ. Mark all answers in MAQ. For data interpretation, pay attention to units, scales. Look above & below the graph, values in x and y axes. Stick to a study plan. Take GRE mock tests, review your mistakes. Maintain a pocket notebook of formulae and shortcuts to go through at the last minute.
Time management plays a very, very crucial role in any timed test like the GRE. Even if you’re well prepared, because of lack of time management techniques, properly, you might end up making mistakes.
Chapter 5
Time Management
How do you go about managing time ? In the table, you can see the number of questions you can expect and how much time we should spend on each question. There’ll be eight to nine questions quantitative comparison questions. These questions should not take more than a minute to be solved.
Numerical entry questions might require an analytical approach so we can afford to set aside a maximum of three minutes for numerical entry questions.
MAQ’s and MCQ’s shouldn’t take more than 1.5 minutes at most.

You might take close to three minutes to solve data interpretation questions. Ideally, you’re going to spend between one and three minutes on any problem. Quantitative comparison questions take less than a minute. But we do suggest you spend a minimum of a minute on these questions even if you complete a question within a minute. Take time to recheck that question. You might go wrong if you do it hastily.
Please be very conscious about this time. When it comes to data interpretation questions, you should absolutely spend three minutes on each problem. We’ll cover this in greater detail moving forward. Numeric entry questions too require about 3 minutes. MCQ and MAQ questions between 1-1.5 minutes. The lower limit for any question is then 1 minute and the upper, 3 minutes.
Best GRE Test Prep out there
Sahitya's score increased by 25 points. See what she has to say!
Show me!Next, do not skip any questions. Follow the mnemonic MIGMO – Make an Intelligent Guess and Move On. There is no negative marking on the GRE. So skipping a question is not going to add any value to your GRE score. So why unnecessarily skip a question? Instead, make an intelligent guess and move on.
Finally, do not use a calculator interface unless required. It takes time to open and plug in values. Moreover, very few questions on the GRE will actually require you to use the calculator. Most require a rational approach. At most, two questions will consist of values so large that the only way to solve it is to use the calculator. As much as possible, avoid using the calculator.
[bctt tweet=”GRE Math Time management : 1) 8-9 quantitative comparison Qs (1 min/Q) 2) Numerical Entry Questions (max 3 mins/Q) 3) MAQs and MCQs (Max 1.5 mins/Q) ” username=”galvanizeprep”]
Chapter 6
GRE Math Technique : PIES
Next, follow the pneumonic PIES to solve word problems. Word problems are often quite large and require you to read many lines. How do you focus on making this easier? Using the ‘PIES’ technique.
This involves ‘P’ – partitioning or breaking the word problem into two parts. I stands for information. E stands for framing an equation. S stands for solving the equation. Essentially, you take a large problem, break it up into easily digestible parts, collect all the information necessary, frame an equation for the same and then solve it.

Let’s look at a simple example. “Alice has twice as much money as Ben. Alive gives Ben 200$. Now Ben has 3 times as much money as Alice has now. What was the amount Alice had initially?”
This is a very simple question but if you read it as a whole, it might seem complicated. So let’s implement PIES. First thing we do is break the problem up. So we know Alice has a certain amount of money ‘A’. B has a certain amount of money ‘B’ initially. Let’s put these values in a table to make it easier.
Now, Alice gives Ben 200$. So Alice now has A-200 whereas Ben has B+200. We have one more statement explaining the relationship between these values. Ben now has three times as much money as Alice does. This means, B+200 = 3(A-200). That’s the final equation we come up with.
Now all you have to do is solve for the equation and you have your answer! That is how you use PIES to simplify word problems for your benefit.
[bctt tweet=”GRE Math Tip: PIES Technique for Word Problems : P-Partition, I – Information, E-Framing Equation, S- Solving Equation” username=”galvanizeprep”]
Chapter 7
Techniques : ZONEF
The next technique we’re going to look at it implementing the ZONEF technique. ZONEF stands for Zero, One, Negative Numbers, Extremes and Fractions. This is applied when you need to plug in values. Mostly this comes of help when you’re working on quantitative comparison questions.
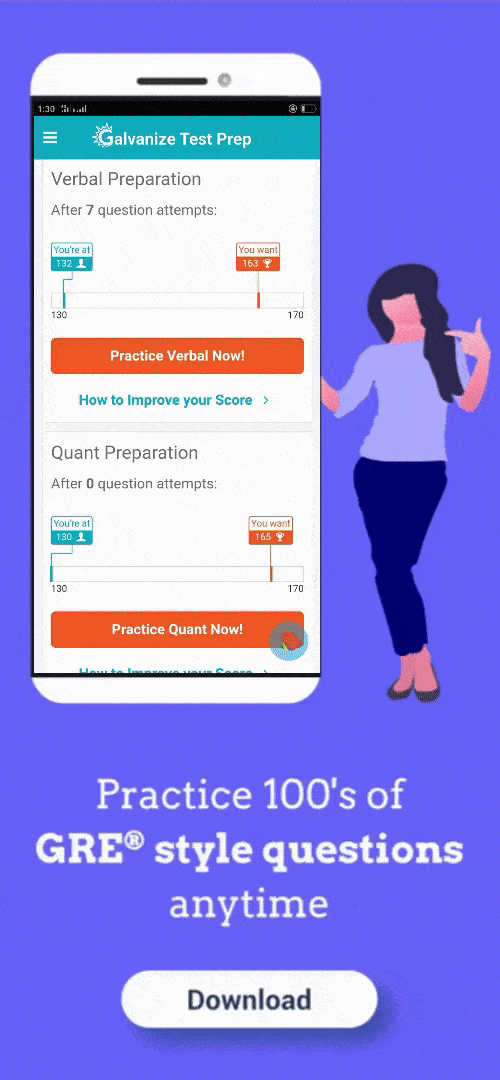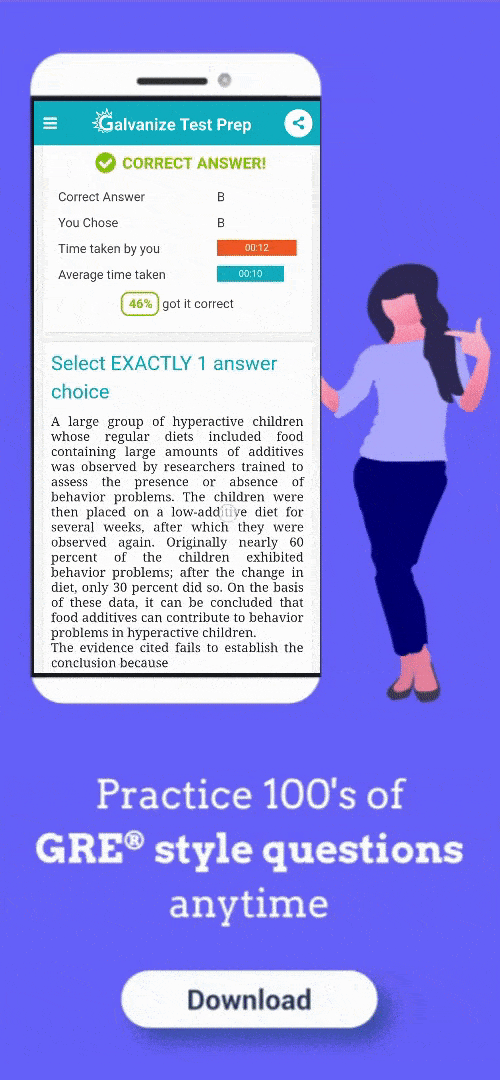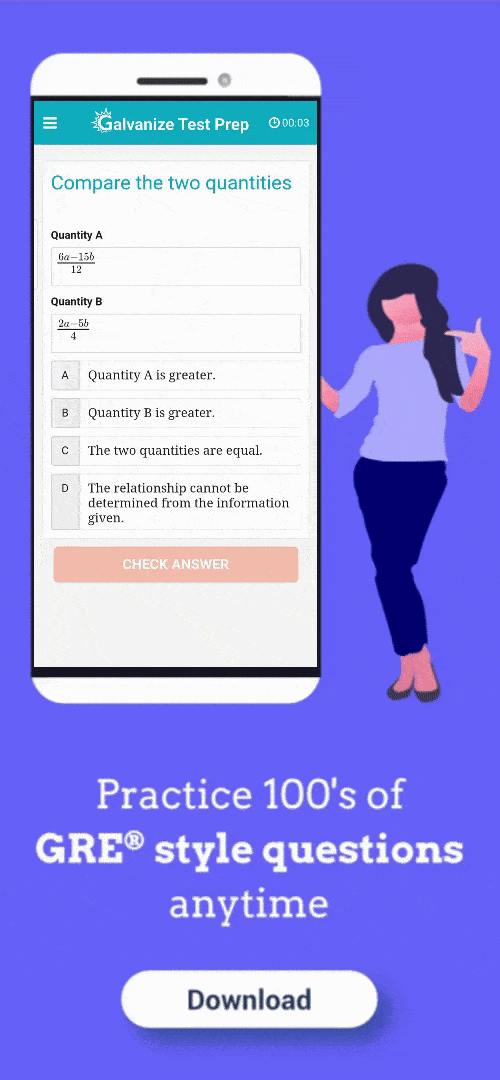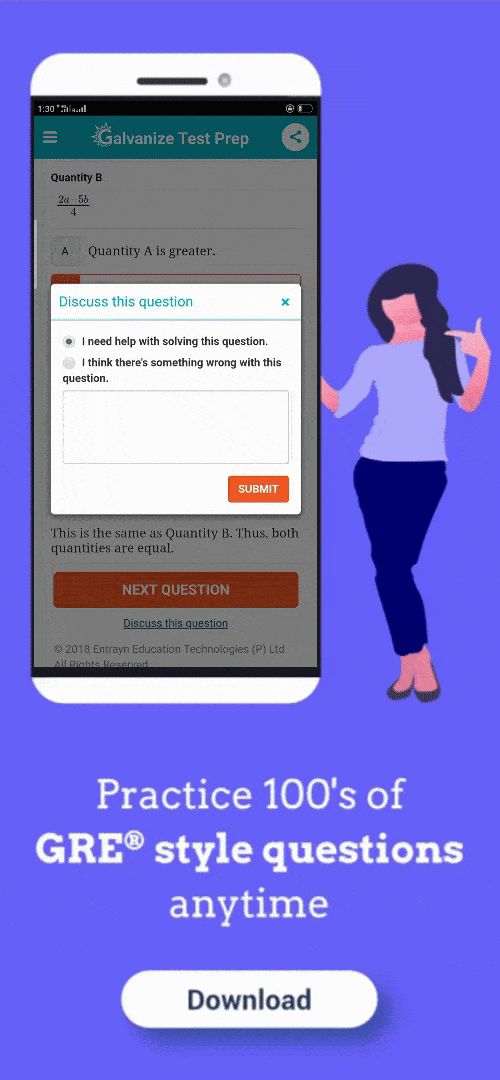
Let’s take a look at a simple example here. x is greater than 0. I have no information about x. I just know that x is greater than zero. You have two quantities – Quantity A and Quantity B. This is a multiple choice question with 4 options always fixed.
A will be Quantity A being greater, B will be Quantity B is greater, the third option will be both Quantity A and B being an equal and the fourth option will always be relationship cannot be determined.

Go for the fourth option only after you analyze in detail about the rest of the 3 options that they do not work out.
Now, how do we apply ZONEF to this? Before we solve this, let’s cover the most common mistakes student tend to make on questions like this. Several test-takers see “x is greater than 0” and plug in the value 1.
If you do that and solve for the equation, you’ll arrive at the conclusion that both values are equal and therefore, the correct answer is option C.
This is wrong. By plugging in a positive integer, you’ve ignored the other possibilities. Of course, in this case, we know its greater than 0 so you can eliminate negative integers. But what about fractions?
Suppose we assume x is ½. Then, in the case of quantity A, 1 divided by 1/4 equals 4. For B – 1 divided by ½ equals 2. Now you’ve arrived at the conclusion that Quantity A> Quantity B. Whereas earlier, we’d seen how by assuming x=1, we arrived at an entirely different conclusion.
So you can see how by plugging in different values, we arrive at different conclusions. Thus, the correct answer here is option D i.e. it cannot be determined.
This was a quantitative comparison question for which we did no calculating. We simply used the ZONEF technique.
[bctt tweet=”GRE Math Technique: ZONEF for quantitative comparison: ZONEF stands for Zero, One, Negative Numbers, Extremes and Fractions” username=”galvanizetest”]
Chapter 8
Using Back-Substitution
Next, let’s look at MCQ’s and MAQ’s. A very common mistake is to do an analytical proof for these. That is an absolute waste of time. Let’s look at an example for the same.
|(2-|x-2|)| = 7. What are the possible values of x in this equation? Many test-takers might panic, looking at the equation. One modulus is confusing enough, there are two here. Now if you apply an analytical approach, you might try squaring them or removing the moduli using the rule ‘mod x is equal to a implies x is equal to plus or minus a.

An easier way to solve this is to back-substitute with the answer choices given. Let’s start with the first option, x=-7.
Substituting the value of x as -7 into the equation |(2-|x-2|)|, we get x=7. Mod of 2-|-9| is 2-9 which equals 7.
Similarly, by substituting the other answer options in the equation and solving in the same manner, we arrive at the other right options. Options B, C and D leave us with the answers 3, 1 and 3. Those are not equal to 7 and so we can know these options are not right. Option E(11) leaves us with 7. Thus, we know options A & E are the right answers in this case.
Another common mistake is to just stop once you have one right answer. But this is an MAQ questions, you’re asked to pick all correct values. If it’s an MCQ question, you need pick only one right option.
But this is an MAQ, you have to pick more than one correct answer. It’s also quite common to get confused between the two. Be very careful solving MCQ’s and MAQ’s – back-substitute. Work back from the answer.
That way you will save time also. This is a very, very important truth and is mostly useful in the case of MAQ’s, MCQ’s and algebra.
Chapter 9
Data Interpretation - Graphs
Another reason test-takers often lose points is that they just glance at the graphs given. This is not helpful. What you need to do is look at the problem statement, look at the scales and units given in the graph. Look at the information given on all the sides of the graph. This is very, very important for data interpretation questions.
Most people involved are automatic percentages. The ratio & proportion. These are the door subtopics that artistic are played in getting into position whenever you interpret a graph.
If you look at the graph in the image, you’ll notice there are two. The first is of the distance traveled in feet against the speed in miles per hour. The second graph contains the same. However, the first is a measurement of the distance traveled in unit time during reaction time. The second is the distance traveled after brakes are applied.
You are special to us
We are Personalized - Study Plan, Course Managers, Feedback & more!
Take me there!So if the question says find the distance traveled during reaction time when the speed is forty, the answer can be found by looking at the graph on the left. If the question says, find the distance traveled by car after the brakes have been applied if the speed fifty miles per hour, you look at the graph on the right.
If, however, it says find the total stopping distance, where do you find that? Below the graph is the information you’re looking for. The total stopping time is the sum of the distance traveled during reaction time and the distance traveled after the brakes have been applied.

So if the question says find the total stopping time when at a speed of 50 miles per hour, you need to look at the corresponding position on the y-coordinates on both graphs and find the sum.
Use a pencil preferably to find the corresponding values in the graphs. That should make it easier to zero in on the right value. Also, keep in mind the speed is given in miles per hour while the distances are mentioned in feet.
Summary: GRE Tips and Tricks
Please read the question and all the information properly. Look at the information given on all sides of the graphs. Data interpretation questions require you to spend up to three minutes.
Three full minutes. So how do you use this time? Allot 2 minutes to read the question and collect all the data given. Use half a minute to read the question and the other half to answer it. It won’t take you longer than that.
Know the format of the GRE Math section in and out. Trust in what you already know. We absolutely do not recommend last-minute preparation.
Finally, always stay positive and focused.
GRE Math Practice Questions
Leave a comment below with the answers to the following questions.
Question 1.
If n is an integer between 1 and 96 (both included), what is the probability that n*(n+1)*(n+2) is divisible by 8.
a. 50%
b. 37.5%
c. 62.5%
d. 12.5%
e. none of these
Question 2.
For an 8-a-side football match, a coach has to choose the team from a squad of 12 boys. Only three of them can play as a goalkeeper and these three cannot play any other position. The other boys can play all the other positions – defense, midfield and forward. If the team should have 1 goal keeper, 3 defenders, 3 midfielders and 1 forward, in how many ways can the coach select the team?
a. 495
b. 108
c. 544320
d. 12580
e. 15120
FAQ: (Frequently Asked Questions)
What is the GRE math syllabus?
- Arithmetic, Algebra, Geometry and Data Analysis
Which topic should be given more weightage in GRE math?
- Arithmetic and data analysis have a lot more weightage in GRE Math. So attend these Qs first followed by the rest : Geometry and Algebra
What are all the mistakes to avoid in geometry section?
- Do not make any assumptions based on visual representations unless it’s mentioned specifically they are up to scale. Read Qs carefully.
What are all the mistakes to avoid in data analysis section?
- People often confuse permutations and combinations. So, have a very strong understanding of permutations, combinations and probability. Practice loads of Questions and make no errors.
What is ZONEF technique?
- ZONEF for quantitative comparison: ZONEF stands for Zero, One, Negative Numbers, Extremes and Fractions
Here’s a Quick Summary :
- GRE Math Syllabus includes topics like : Arithmetic, Algebra, Geometry and Data Analysis. Proper understanding of these topics with enough practice will get you to your perfect 170
- Arithmetic and data analysis have a lot more weightage in GRE Math. So attend these Qs first.
- GRE is a skill based exam and so how well you do in GRE depends on how well you understood the concepts.
- Mistakes in GRE Math : Calculation Error and Conceptual Errors. Also make sure to read the questions very carefully and be careful while rounding off answers
- GRE Math Section: Numeric Entry, MCQ’s, MAQ’s and Quantitative Comparison Questions
- In the Geometry Section : Do not make any assumptions based on visual representations unless it’s mentioned specifically they are up to scale. Read Qs carefully.
- In Data Analysis Questions, Have a very strong understanding of permutations, combinations and probability. Practice loads of Questions and make no errors.
- GRE Math Techniques
- Read Qs Properly
- Avoid Calculation and Conceptual Mistakes
- Time Management
- Implement ZONEF,PIES
- Apply shortcuts and approximations
- Back Substitute in MCQ and MAQ
- Data Interpretation : Pay attention to units, scales,look above and below the graph, Values in x and y axes
- Stick to our study plan
- Take the mock tests
- Review your mistakes
- Maintain a pocketbook of formulas and shortcuts
- GRE Math Time management :
- 8-9 quantitative comparison Qs (1 min/Q)
- Numerical Entry Questions (max 3 mins/Q)
- MAQs and MCQs (Max 1.5 mins/Q)
- GRE Math Tip : Make sure you spend a minimum of a minute on these questions even if you complete a question within a minute. Take time to recheck that question.
- GRE Math Tip : Don’t skip any questions since there are no negative markings. MIGMO : Make an intelligent guess and move on
- GRE Math Tip : Don’t use calculator unless required : It consumes time
- PIES Technique for Word Problems : P-Partition, I – Information, E-Framing Equation, S- Solving Equation
- ZONEF for quantitative comparison: ZONEF stands for Zero, One, Negative Numbers, Extremes and Fractions
- Back substitution method for MCQs and MAQs : The age old method still works! Substitute and check if the answer matches the equation
Related Blogs
- GRE Reading Comprehension | With Practice Questions and Answer’s
- How to Score a 160+ on the GRE Verbal | Tips, Pattern, Practice Questions & Scores
- A Killer Guide to Analytical Writing Assessment | With Samples for Practice
- GRE 101: A Complete Guide To GRE
- Free Online GRE Practice Test with Score Analysis
- GRE Quant :Time Management Tips
- All You Need To Know About GRE Vocabulary
now it's your turn
I'd like to hear from you
Which strategy from today’s guide do you think will work best for you?
Are you going to working on your time management skills right away?
Or maybe you’re ready to start using shortcuts.
Either way, leave a comment below right now.














B
Great attempt! But, the right answer is C.
So when the larger cube is cut into smaller cubes, the corner cubes will have paint on three sides.
The cubes in the middle of the faces will have paint on only one side, but the cubes cut from the edges will have paint on two sides.
In this case, there will be only one cube one each edge (excluding the corners), and since there are 12 edges, there will be 12 cubes with paint on two sides. (Drawing a diagram will make this much clearer.)
Ans: C
The answer is C
c
good one
nice one
C
Great
Really helpful !
Great info!
C
Absolutely, the answer is C.
Well, what a very detailed tips that I’ve never found previously. It makes sense and can’t wait to practise them. Thank you.
Cool
Excellent
Answer is c
Very helpfull blog
great
Very beneficial
Nice